Welcome to the new curecoinfolding.com! In honor of the best place to get artificially-flavored, tongue-staining drinks on the cheap, 7/11/2014 marks the date of this blog’s rebirth-from the ashes of hardware reviews and software tips into everything under the sun related to Curecoin as a whole.
For anyone unfamiliar with Curecoin, check out our website: curecoin.net. Curecoin aims to merge cryptocurrency with computational research, currently centered around protein folding utilizing Stanford’s Folding@Home project. We are no affiliated with Stanford.
This blog will be updated once or twice a week with the latest internal ramblings of the dev team, any exciting developments in Curecoin’s growth, and anything else worthy of mention. At present, we have finalized most of the materials for the conference, here’s a quick preview of the banners that will appear at our table:

In an unrelated tangent, I made a post on the bitcointalk forums about alternatives to ECDSA public/private key pairs. To summarize (full post: Lamport and Lamport-esque Signatures) Bitcoin uses ECDSA for generating addresses and for signing transactions. When you create a Bitcoin (or any other derivative currency) address, your wallet generates a public/private key pair, and then uses the public key to create an address with the help from irreversible hashing functions:
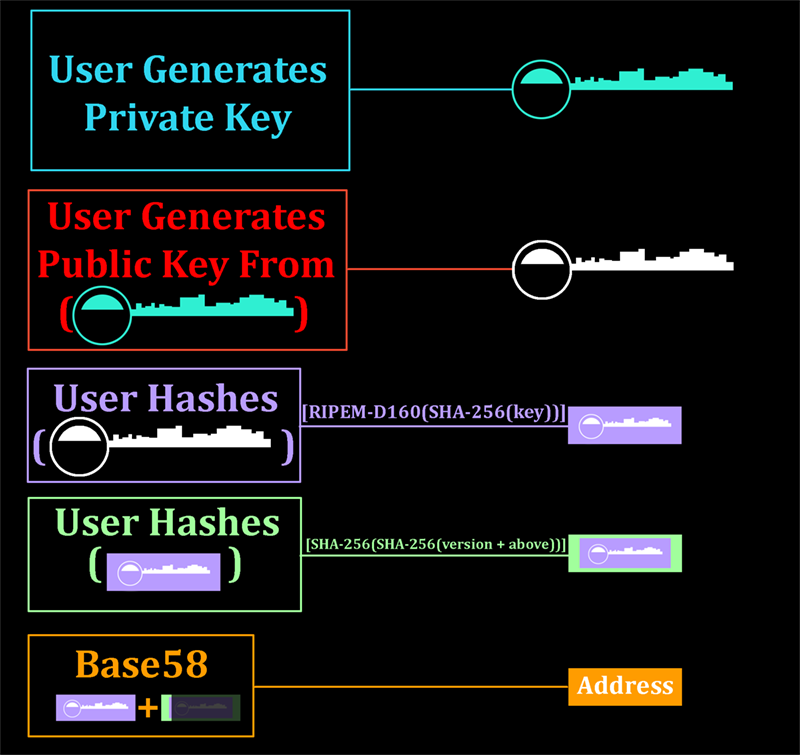
ECDSA, like many other public/private key algorithms implemented widely today, relies on one or more mathematical algorithms which are considered ‘hard’ to do in reverse (by hard, I mean the collective computational power of the world would take longer than the age of the universe to do the function in reverse properly). Such algorithms include the prime factorization of large numbers. In many cases this hardness refers only to classic computational methods-where we are working with ones OR zeroes. Quantum computing introduces algorithms like Shor’s algorithm, which, with a small modification, could attack ECDSA public keys, revealing the private key to an unauthorized third party. The private key should, as its name hopefully implies, stay private. You use it when you sign a Bitcoin transaction, but you never actually reveal it to the network, just like you never teach someone how to forge your signature on checks. This private key is stored in your wallet.dat file. However, upon signing a message, other participants on the network need to verify that you actually signed it. As such, you have to reveal your public key the first time an address spends Bitcoin (it was previously protected behind the figurative mask of hashing functions). This public key is first re-computed into an address by the network, and if it matches your address, the signature is checked against the public key. If that too matches, then you (or someone with your wallet) signed off on a transaction, and the network validates the transaction.
As such, an address on the Bitcoin network is not vulnerable to quantum computer attacks until it signs a transaction. However, after you sign one transaction with an address, your public key is revealed, and anyone with the ability to run Shor’s algorithm would be able to derive your private key and spend your Bitcoins. While one can safely assume that no powerful quantum computers exist today, the chance that a third party building a successful quantum computer might find lack of vocalization of their achievement to be the most personally beneficial route is high-leaving cryptos with little or no time to prepare and transition to a quantum-computer-resistant signature mechanism.
Due to the nature of quantum computing, hashing functions (like SHA256 or RIPEMD-160, which ‘lose’ data while the algorithm runs) are quantum-computing-proof, and thus are prime candidates for being used in a signing algorithm resistant to quantum computing attacks. A mechanism for signing a single message using hashing functions has existed for decades, and is known as the Lamport Signature Scheme (Lamport Signing @ Wikipedia). This method has a few intrinsic flaws which make it impractical for cryptocurrency transaction verification and address generation:
-> One-time signatures (would require either address chaining or changing addresses every transaction)
-> Large public key
-> Large signature footprint
The first issue can be resolved by creating a Merkle Tree: (Merkle Signing @ Wikipedia)
The second issue can be resolved by using a public key that is a hash of the normal public signature. Additionally, the top level of the Merkle Signature Tree above could be used as a public key, and would have a footprint the length of the hashing function.
The third issue is much harder to tackle, however it has been attacked by CMSS (https://eprint.iacr.org/2006/320.pdf). Even with a system such as CMSS in place, the signature alone occupies multiple kilobytes. This size could be further reduced by using smaller hashing functions, by using standard compression for storage, and by implementing partial-chain clients, who would work in P2P clusters to share signature information when needed.
There is no promise that Lamport-esque signature schemes will be implemented in Curecoin now or in the future, it is simply a proposed solution to the quantum computing problem that the Curecoin developers are further investigating.